Определение 5.1. Произведением вектора 
на действительное число 
называется вектор 
, который удовлетворяет двум условиям:
1. 
;
2. 
, если 
и
, если 
.
Из условия 1. следует, что 
тогда и только тогда, когда 
или 
.
В дальнейшем вместо записи 
будем употреблять запись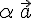 
Напомним определение гомотетии, известное из школьного курса геометрии.
Определение 5.2. Гомотетией с центром в точке 
и коэффициентом 
называется такое преобразование плоскости, при котором каждой точке 
ставится в соответствие точка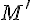 
такая, что выполнены следующие условия:
1. точки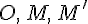 
лежат на одной прямой;
2. 
;
3. 
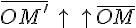, если 
и
, если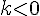 
.
Предварительно докажем одну лемму.
ЛЕММА 5.1. Если при гомотетии с центром в точке и коэффициентом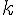 
треугольник 
переходит
в треугольник 
, то 
.
Доказательство. По определению гомотетии имеем 
и 
, поэтому 
подобен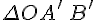 
с коэффициентом 
. Отсюда следует, что 
и 
. Если 
, то точки 
и 
лежат по одну сторону от прямой 
, поэтому 
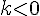, следовательно, . Если , то точки и лежат по разные стороны от прямой , поэтому 
, т.е. и в этом случае .
