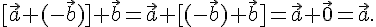Определение 4.1. Разностью векторов 
и 
, взятых в данном порядке, называется такой вектор 
, который в сумме со вторым вектором дает первый вектор.
Докажем существование и единственность разности.
Существование. Отложим векторы и от одной и той же точки 
:
Применяя равенство 
для точек 
получаем
Полагая 
, будем иметь 
. Этим доказано существование разности.
Единственность. Пусть существует еще вектор 
такой, что 
. Тогда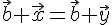 
. Прибавим к обеим частям этого равенства вектор 
. Получим
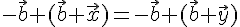
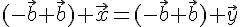
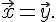
Таким образом, доказано существование и единственность разности любых двух векторов, при этом эта разность обозначается 
.
Замечание 4.1. Из доказательства существования разности векторов можно сформулировать правило нахождения разности двух векторов:
Разностью двух данных векторов, отложенных из одной точки является вектор, идущий из конца второго в конец первого.
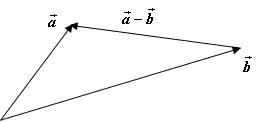
Отметим еще равенство
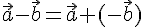
В самом деле,
