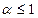Свойства алгебраических операций.

Пусть А, В, С - нечёткие множества. Тогда для них выполняются следующие свойства:

Коммутативность: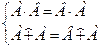

Ассоциативность: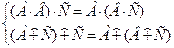

Формулы де Моргана: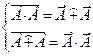

А

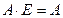
, где О - пустое множество

Е - универсальное множество

Для алгебраических операций над нечеткими множествами не выполняются свойства:

Идемпотентность: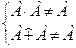

Дистрибутивность: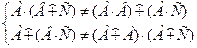

Кроме того

,

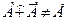
При совместном использовании логических операций (объединение и пересечение) и алгебраических операций справедливы свойства

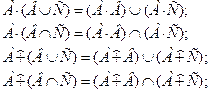
Возведение в степень

>0 Нечёткое множество определяется функцией принадлежности

Частные случаи возведения в степень:

Концентрирование (уплотнение)

CON(A) = A² ( нечеткий модификатор типа «очень»)

Растяжение (рисунок 30)

DIL(A) = A^0.5 (нечеткий модификатор типа «почти»)

Умножение на число

Если >0, такое, что max m_А(х) 1, то нечёткое множество имеет

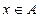
функцию принадлежности .

Нечёткое множество -уровня.