Элементарными преобразованиями над строками матрицназываются следующие преобразования строк:
1. умножение строки на ненулевое число;
2. перестановка двух строк;
3. прибавление к одной строке матрицы другой ее строки, умноженной на некоторое ненулевое число.
Если от матрицы 
к матрице 
перешли с помощью эквивалентных преобразований над строками, то такие матрицы называются эквивалентными и обозначают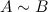 
.
Примеры элементарных преобразований
Продемонстрируем все элементарные преобразования на примере матрицы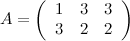 
Умножим первую строку матрицы на два, то есть каждый элемент первой строки умножаем на двойку, в результате получим матрицу , эквивалентную заданной матрице :
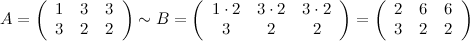
Поменяем первую и вторую строки матрицы местами, получаем эквивалентную ей матрицу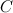 
:
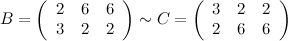
От первой строки матрицы 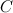отнимем вторую строку, получаем эквивалентную матрицу 
:
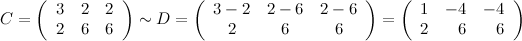
В итоге делаем вывод, что матрицы и эквивалентны, так как от одной из них перешли к другой при помощи эквивалентных преобразований над строками.
Понятие определителя матрицы
