МАТРИЦЫ
Оглавление.
1. Определение матриц.
2. Квадратные матрицы.
3. Действия с матрицами
4. Ранг матрицы.
5. Обратная матрица.
Системы линейных уравнений.
А. Метод Гаусса.
6.б. Формулы Крамера.
6.в. Матричный метод.
Системы линейных уравнений общего вида.
Определение матриц
Прямоугольная таблица, содержащая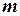 
строк и 
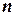столбцов, называется матрицей размера 
.
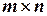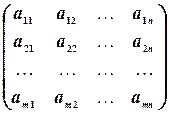
Числа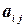 
называются элементами матрицы. Каждый элемент матрицы снабжен двумя индексами: первый индекс указывает номер строки, второй — номер столбца, в котором расположен этот элемент.
Матрицы обозначают буквами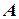 
, 
, 
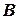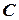и т. д. Например,
или сокращенно в виде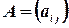 
.
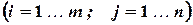Две матрицы 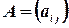и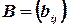 
считаются равными, если равно число их строк и число столбцов и если равны элементы, стоящие на соответствующих местах этих матриц равны, то есть 
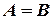, если 
.
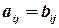Часто приходится рассматривать матрицу, столбцами которой являются строки матрицы 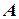. Эта матрица называется транспонированной к 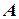и обозначается через 
.
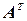Пусть дана матрица 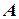. Переставим строки со столбцами. Получим матрицу
,
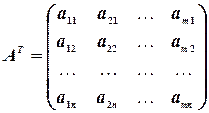которая будет транспонированной по отношению к матрице .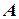
