Определение 12. Проекцией точки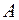 
на ось 
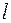называется точка пересечения плоскости 
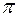, проходящей через точку 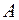перпендикулярно оси 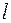с осью 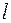(рис. 15).
Рис. 15
Определение 13. Проекцией вектора 
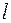на ось называется число, равное разности координат проекций конца и начала (рис. 16).
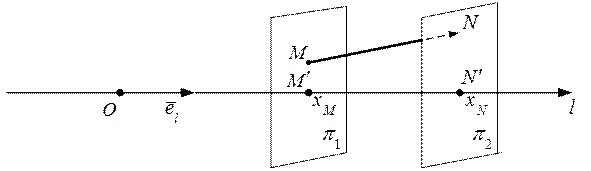
Рис. 16
Проекция вектора на ось 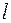обозначается 
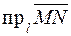. Имеем
.
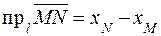Обозначим через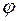 
угол между вектором и осью .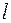
Проекция вектора может быть: 1) положительной, если угол 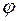острый. В этом случае 
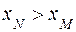(рис 16), 2) отрицательной, если угол 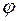тупой. В этом случае 
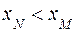(рис. 17), 3) нулевой, если угол 
или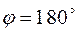 
. В этом случае 
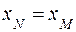(рис. 18).
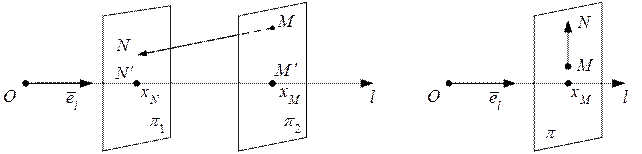
Рис. 17 Рис. 18
Определение 13. Составляющей вектора по оси 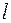называется произведение проекции вектора на ось 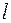на единичный вектор 
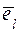этой оси и обозначается 
.
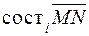Составляющей вектора по оси 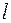есть вектор, соединяющий проекцию начала и проекцию конца вектора:
.
Отметим некоторые свойства проекции вектора на ось.
Свойство 1. Проекция вектора 
на ось 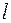равна произведению длины вектора на косинус угла между вектором и осью :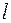
.
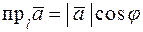Свойство 2. Проекция произведения вектора на число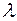 
на ось 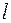равна произведению числа 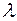на проекцию вектора на ось :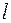
.
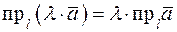Свойство 3. Проекция суммы двух векторов и 
на ось 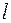равна сумме проекций этих векторов на ось :
.
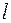Свойство 4. Проекция разности двух векторов и на ось 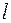равна разности проекций этих векторов на ось :
.
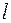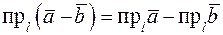