Числовым рядом называется сумма вида
, (1)
где 
называемые членами ряда, образуют бесконечную последовательность; член 
называется общим членом ряда.
Суммы:
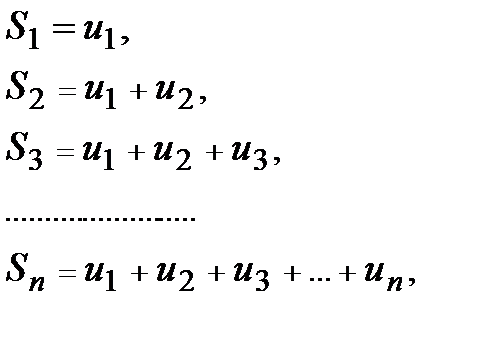
составленные из первых членов ряда (1), называются частичными суммами этого ряда.
Каждому ряду можно сопоставить последовательность частичных сумм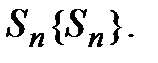 
Если при бесконечном возрастании номера n частичная сумма ряда 
стремится к пределу S, то ряд называется сходящимся, а число S – суммой сходящегося ряда, т.е.
и 
.
Эта запись равносильна записи
.
Если частичная сумма ряда (1) при неограниченном возрастании n не имеет конечного предела (стремится к 
или 
), то такой ряд называется расходящимся.
Задание 1. Найти общий член числового ряда:
1) 
2) 
3) 
4) 
5) 
| 6) 
7) 
8) 
9) 
10) 
|
