С.В. Галкин
Математический анализ
(Методические указания
По материалам лекций для подготовки
К экзамену в четвертом семестре).
Часть 1 Ряды Фурье.
Этот раздел может быть перенесен в третий семестр как продолжение темы «Функциональные ряды». Но часто в третьем семестре не хватает времени, поэтому материал может быть изложен и в четвертом семестре.
Лекция 1. Задача о наилучшем приближении.
Задача о наилучшем приближении в Rn.
Поставим задачу – приблизить наилучшим образом вектор трехмерного пространства вектором v в двухмерном пространстве - плоскости.
Ясно, что интуитивно наилучший выбор v – ортогональная проекция вектора uна эту плоскость. Пусть e1 , e2– ортогональные базисные векторы, а плоскость – их линейная оболочка, тогда v =C1 e1 +C2 e2.Остается найти коэффициенты разложения C1, C2.
Если v – ортогональная проекция вектора uна плоскость, то вектор u – vортогонален плоскости, следовательно, ортогонален и базисным векторам. Тогда
0 = (u --v, e1) =([u – (C1 e1 +C2 e2)], e1) = (u, e1) –C1 (e1, e1), 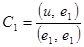
0 = (u --v, e2) =([u – (C1 e1 +C2 e2)], e2) = (u, e2) –C2 (e2, e2),  .
.
Здесь(e1, e2) = 0,так как базисные векторы ортогональны.
Аналогично решается задача наилучшего приближения вектора из Rn+1 вектором из Rn: Наилучший выбор приближения – проекция вектора на Rn.
V =C1 e1 +…Cn en,где  .
.