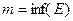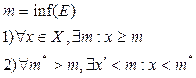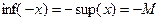|
|
ПаскальСиАссемблерJavaMatlabPhpHtmlJavaScriptCSSC#DelphiТурбо Пролог1С Компьютерные сетиСистемное программное обеспечениеИнформационные технологииПрограммирование Linux Unix Алгоритмические языки Аналоговые и гибридные вычислительные устройства Архитектура микроконтроллеров Введение в разработку распределенных информационных систем Введение в численные методы Дискретная математика Информационное обслуживание пользователей Информация и моделирование в управлении производством Компьютерная графика Математическое и компьютерное моделирование Моделирование Нейрокомпьютеры Проектирование программ диагностики компьютерных систем и сетей Проектирование системных программ Системы счисления Теория статистики Теория оптимизации Уроки AutoCAD 3D Уроки базы данных Access Уроки Orcad Цифровые автоматы Шпаргалки по компьютеру Шпаргалки по программированию Экспертные системы Элементы теории информации |
Множини й дії над ними.Дата добавления: 2015-08-14; просмотров: 1015; Нарушение авторских прав
Число х називається координатою точки М. Найбільше використовівані наступні числові множини: 1) множина всіх чисел, що задовольняють нерівності 2) множина всіх чисел, що задовольняють строгій нерівності 3) множина всіх речовинних чисел позначають 4) множини виду Ці множини називаються проміжками: відрізки, інтервали й напівінтервали називаються кінцевими проміжками, числа a і b – їхніми кінцями, інші – нескінченними. Обмежені множини 1. 2. 3. Якщо множина Е обмежена зверху, то числа З такі, що Найменше серед верхніх граней називається найменшою верхньою гранню й позначається
Якщо множина Е обмежена знизу, то числа d такі, що Найбільше серед нижніх граней називається найбільшою нижньою гранню й позначається
Завдання для перевірки знань:
Література: 1. «Высшая математика для экономистов» под редакцией Н.Ш. Кремера стр.123-124 2. М.І. Шкіль «Математичний аналіз» стр. 10-33 3. В.М. Лейфура, Г.І. Городницький, Й.І. Фауст «Математика» стр.5-11
Додаткова література: 1. А.Д. Мышкис «Лекции по высшей математике» стр.12-24 2. Л.Д. Кудрявцев «Курс математического анализа» том 1 стр. 5-13
|
||||||||||||||
Уроки php mysql Программирование
Онлайн система счисления Калькулятор онлайн обычный Инженерный калькулятор онлайн Замена русских букв на английские для вебмастеров Замена русских букв на английские
Аппаратное и программное обеспечение
Графика и компьютерная сфера
Интегрированная геоинформационная система
Интернет
Компьютер
Комплектующие компьютера
Лекции
Методы и средства измерений неэлектрических величин
Обслуживание компьютерных и периферийных устройств
Операционные системы
Параллельное программирование
Проектирование электронных средств
Периферийные устройства
Полезные ресурсы для программистов
Программы для программистов
Статьи для программистов
Cтруктура и организация данных

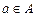 . Нехай X і Y – обоє множини. Між ними можна визначити наступні співвідношення: дві множини називаються рівними, якщо вони складаються з тих самих елементів; якщо всі елементи множини Х утримуються в множині Y, та множина Х називається підмножиною множини Y і позначається
. Нехай X і Y – обоє множини. Між ними можна визначити наступні співвідношення: дві множини називаються рівними, якщо вони складаються з тих самих елементів; якщо всі елементи множини Х утримуються в множині Y, та множина Х називається підмножиною множини Y і позначається 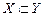 .
.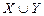 .
.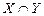 .
.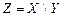 .
.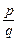 , де p і q – цілі числа, і ірраціональних.
, де p і q – цілі числа, і ірраціональних.
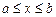 називається відрізком
називається відрізком 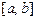 ;
;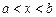 , називається інтервалом
, називається інтервалом 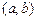 ;
;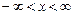 або
або 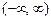 ;
;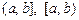 – напівінтервали,
– напівінтервали, 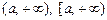 ,
, 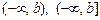 .
.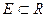 обмежено зверху
обмежено зверху 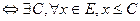
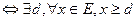
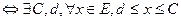
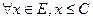 називаються верхніми гранями, їхня нескінченна множина, найбільших серед них нема, найменше є.
називаються верхніми гранями, їхня нескінченна множина, найбільших серед них нема, найменше є.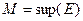
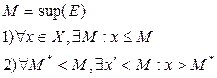
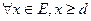 називаються нижніми гранями, їхня нескінченна множина, найменших серед них нема, найбільше є.
називаються нижніми гранями, їхня нескінченна множина, найменших серед них нема, найбільше є.