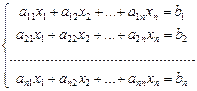Рассмотрим матрицу А: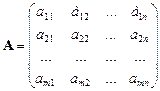 
Выделим в матрице k строк и k столбцов (k<=min(m,n)). Из элементов, стоящих на пересечении выделенных строк и столбцов составим определитель k-го порядка. Такие определители называются минорами k-го порядка этой матрицы. В нашей матрице выделен минор 2-го порядка.
Наибольший порядок миноров данной матрицы отличных от нуля наз. рангом матрицы
Обозначается r(A), rang(A),r. Очевидно, что r< min(m,n). Минор, порядок которого определяет ранг матрицы наз. базисным.
Свойства ранга матрицы:
1. При транспонировании матрицы ее ранг не меняется
2. Если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменится
3. Ранг матрицы не меняется при элементарных преобразованиях
Системы 2-х и 3-х линейных уравнений .
Пусть мы умеем вычислять определители (n-1)-го порядка и задана квадратная матрица n-го порядка
. Тогда определителем матрицы А (определителем n-го порядка) называется число, не зависящее от номера строки по которой разлагается определитель: 
. Аналогично определитель n-го порядка можно разложить и по j–му столбцу: 
. Где 
алгебраическое дополнение элемента 
.
С помощью определителей n-го порядка можно исследовать системы линейных уравнений с n неизвестными.
Рассмотрим систему линейных уравнений n-го порядка:
