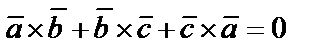1) Для того чтобы вектора 
были компланарны, необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.
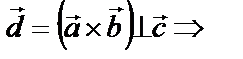
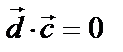
Рис.5.9.
2) Для любых векторов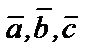 
или
Смешанное произведение не изменяется при круговой перестановке векторов 
и 
и меняет свой знак при других перестановках
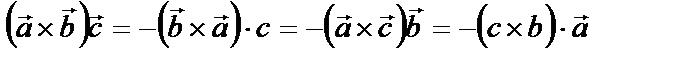
Рис.5.10.
Правило проще запомнить с помощью рисунков 5.10.
3) Смешанное произведение дистрибутивно:
.
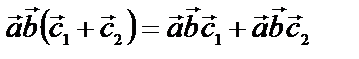
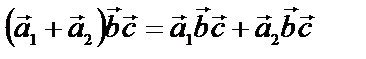4) Ассоциативно относительно умножения на число
, 
, 
.
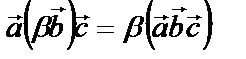5) Смешанное произведение в координатной форме
Пусть даны вектора 
в разложении по базису 
, 
, 
.
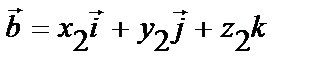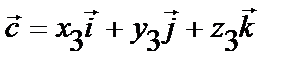
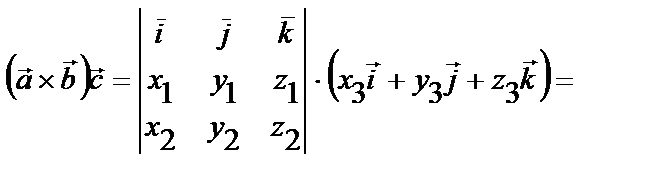
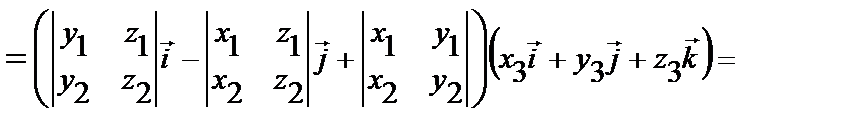
Отсюда следует условие компланарности векторов 
в координатной форме: 
.
Пример5.9.1. Показать что векторы 
, 
, 
компланарны.
Решение: Составим определитель из координат данных векторов и найдем его значение.
.
Ответ: Вектора 
компланарны.
Контрольные вопросы и задания.
1. Дайте определение смешанного произведения.
2. Перечислите свойства смешанного произведения.
3. Геометрический смысл смешанного произведения.
4. Запищите условие компланарности трех векторов в координатной форме.
5. Определить какой является тройка ортов 
прямоугольной декартовой системы координат.
6. Вывести условие принадлежности четырех точек одной плоскости.
7. Доказать компланарность векторов 
,зная что 
