Пусть даны три вектора 
. Вектор 
умножается векторно на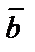 
, полученное векторное произведение 
умножим скалярно на 
, в результате получим число, которое называют векторно-скалярным или смешанным произведением трех векторов 
.
Определение 5.8.1. Смешанным произведением векторов 
называется число, равное скалярному произведению вектора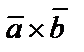 
на вектор 
: 
, или 
или 
.
Геометрический смыл смешанного произведения
Теорема 5.8.1. Смешанное произведение 
трех некомланарных векторов 
, равно объему параллелепипеда, построенного на этих векторах, взятому со знаком плюс, если тройка ( 
) правая, и со знаком минус, если эта тройка — левая.
Доказательство: Сначала рассмотрим случай, когда вектора 
лежат на одной прямой. В этом случае 
, значит и 
. Если же вектора не лежат на одной прямой и вектор 
лежит в плоскости, определенной векторами , то вектор 
ортоганален вектору и, следовательно, . Пусть вектора 
не лежат в одной плоскости и образуют правую тройку. На векторах, как на ребрах, построим параллелепипед.
По определению скалярного произведения
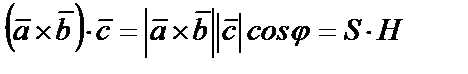
S- площадь основания OBDA, H– высота параллелепипеда.
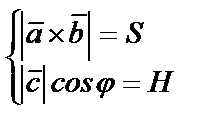
Если 
то 
и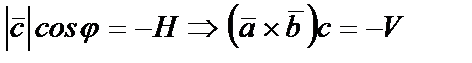 
Окончательно: 
или 
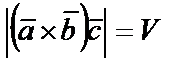
Рис.5.8.
