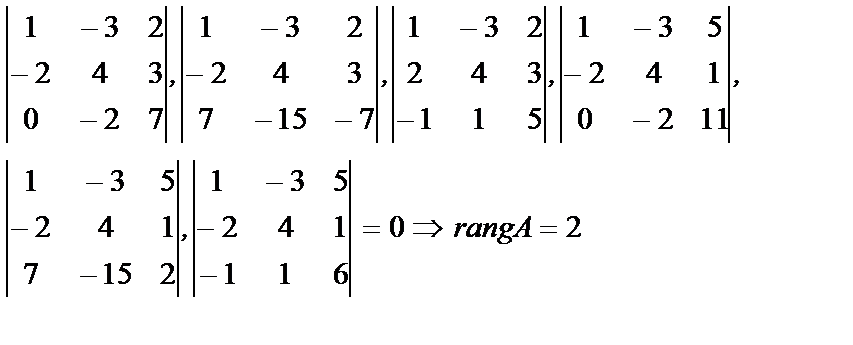Наивысший порядок отличного от нуля минора матрицы Аmxn называется рангом этой матрицы и обозначается как rangA или r(А)
Если А - нулевая матрица то r(А)=0
Поскольку r(А) – порядок минора то очевидно следующее утверждения:
1) rangАmxn Ј min(m,n)
2) rangАnxn = nЫ¦А¦№ 0
Определение 1.8.2.
Если rangАmxn Ј min(m,n) то матрица А называется матрицей полного ранга
Если матрица не полного ранга то утверждение RangА=2 означает что $ Мr№0, а любой минор большего порядка равен 0
Следовательно для определения ранга матрицы достаточно найти минор отличный от нуля ,все окаймляющие миноры которого равны нулю.
Пример1.8.1.
Найти ранг матрицы 
.
Решение:
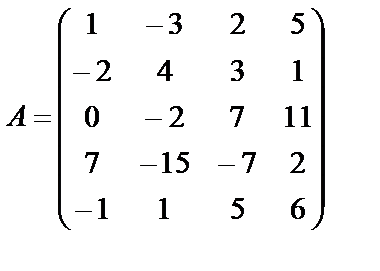
Возьмём "отличный то нуля элемент , пусть а11=1 то М1№0. Окаймляющий его минор ,
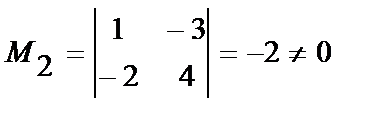Среди миноров окаймляющих М2 нет отличных от нуля:
