Пусть задана функция y = f (x),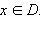 
Тогда каждому числу 
соответствует единственное число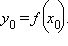 
Иногда приходится по значению функции y0 находить значение аргумента x0, то есть решать уравнение f (x) = y0 относительно x. Это уравнение может иметь несколько или даже бесконечное количество решений (решениями являются абсциссы всех точек, в которых график y = f (x) пересекается с прямой y = y0).
Если функция f такова, что каждому значению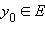 
соответствует только одно значение 
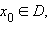то эту функцию называют обратимой. Для такой функции уравнение y = f (x) можно при любом y однозначно разрешить относительно x, то есть каждому 
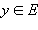соответствует единственное значение 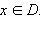Это соответствие определяет функцию, которую называютобратной к функции f и обозначают символом f–1.
Пусть g = f–1. Тогда:
- D (g) = E (f), E (g) = D (f);
- для любого
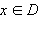g (f (x)) = x, - для любого
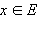f (g (x)) = x; - графики функций y = f (x) и y = g (x) симметричны друг другу относительно прямой y = x.
|
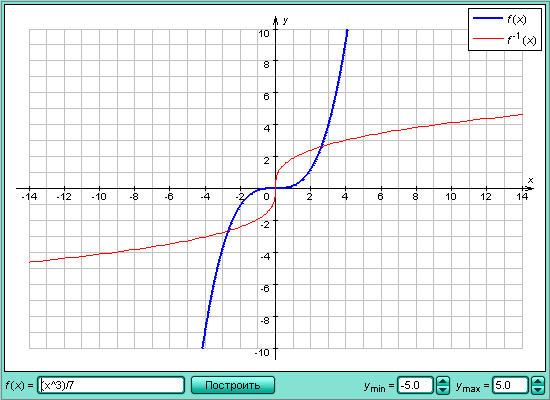
| Модель 1.11. Обратные функции
|
