Суммой 
двух векторов 
и 
называется вектор, который получается из векторов
и по правилу треугольника или по правилу параллелограмма:
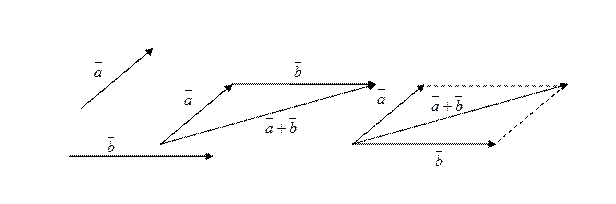
Операция сложения векторов обладает следующими свойствами:
1.Сложение векторов коммутативно: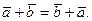 
2.Сложение векторов ассоциативно: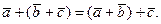 
3.Для любых двух векторов имеет место неравенство треугольника:
£ 
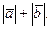
Вектор, равный вектору по длине и противоположно направленный, называется противоположным вектором для вектора и обозначается 
.
Разностью 
векторов и называется сумма векторов и 
, т. е.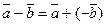 
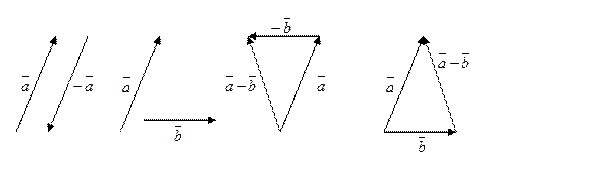
Произведением вектора на действительное число 
называется вектор 
, длина которого 
, а направление совпадает с направлением вектора , если 
и противоположно ему, если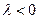 
.
Из определения произведения вектора на число, следует, что два вектора и коллинеарны тогда и только тогда, когда имеет место равенство: 
.
Операция умножения вектора на число обладает следующими свойствами:
l,mÎR
1) l(m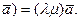 
2) 
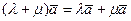
3) 
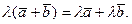
Если 
, то
,
,
.
Признаком коллинеарности двух векторов и является пропорциональность их координат: 
.
Пример 1.
Даны векторы 
и l=3.
Найти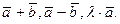 
Решение. Пользуясь свойствами суммы ,разности векторов и произведения вектора на число, получаем:
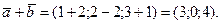
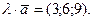
Пример 2.
Коллинеарны ли векторы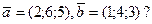 
Решение.
т.к. соответствующие координаты не пропорциональны, то векторы не коллинеарны.
