Найдем смешанное произведение векторов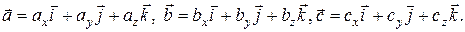 
Таким образом, смешанное произведение численно равно определителю, составленному из координат векторов, т.е.
.
Некоторые приложения смешанного произведения.
1. Определение взаимной ориентации векторов: если смешанное произведение положительно, вектора образуют правую тройку, если произведение отрицательно, тройка отрицательная.
2. Установление компланарности векторов: вектора 
компланарны тогда и только тогда, когда их смешанное произведение равно 0, т.е. 
.
3. Объёмы параллелепипеда и пирамиды: Объём параллелепипеда равен модулю смешанного произведения векторов , которые совпадают с ребрами параллелепипеда, имеющими общую вершину, т.е. 
, и, соответственно, объём призмы, равен одной шестой модуля смешанного произведения, т.е. 
.
Пример 7. Вершинами пирамиды служат вершины A(1;2;3), B(0;-1;1), C(2;5;2),
D(3;0;-2). Определить ориентацию векторов 
Найти объём пирамиды.
Найдем координты векторов.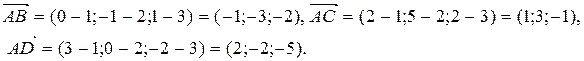 
Вычислим смешанное произведение найденных векторов.
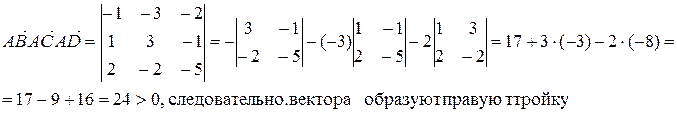
Объём пирамиды равен одной шестой от смешанного произведения, т.е.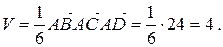 
Поскольку смешанное произведение положительно, вектора 
образуют правую тройку.
