Пусть функции 
и 
и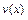меют в точке 
конечную производную, причем 
. Тогда:
1) 
, где 
- любые постоянные;
2) 
;
3) 
.
Эти правила распространяются на любое конечное число слагаемых или сомножителей.
В частности, если 
, то
.
В общем виде, если 
, то
.
Теорема о дифференцировании сложной функции.
Пусть функция 
имеет производную 
, а функция 
имеет производную 
в точках . Тогда производная сложной функции 
находится по формуле
, 
.
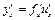Определение дифференцируемости функции.
Функция 
называется дифференцируемой в точке , если её приращение в этой точке представимо в виде:
,
где 
, а 
при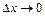 
.
Очевидно, что второе слагаемое в этом равенстве может быть записано в виде: 
.
Имеет место следующая теорема:
