Метод исключения Гаусса.

Численные методы решения СЛУ часто базируются на методе исключения Гаусса. Это один из лучших среди известных алгоритмов, и он основывается на том факте, что сложение одного уравнения с другим, возможно умноженным на константу, не изменяет решения системы.

Рассмотрим матричное уравнение и перепишем его в координатной форме, обозначив элементы b_i вектора b через а_i, _n+1 — это упростит дальнейшее обозначение. Сперва в системе уравнений 1-го порядка производят исключение X₁.

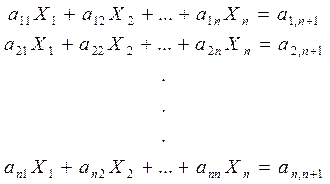
1. Разделим первое уравнение на а₁₁, получим

Х₁+а⁽¹⁾₁₂Х₂+а⁽¹⁾₁₃+ ... =а⁽¹⁾₁,_n+1 (обозн. a⁽¹⁾₁₂=a₁₂/a₁₁) и т. д.

2. Умножим это уравнение на -а₂₁ и сложим его со 2-м исходным уравнением. a⁽¹⁾_2j=a_2j-a₂₁a⁽¹⁾_1j , j = l , 2 , ... , n + l

3. Аналогично для других уравнений подставка

A⁽¹⁾_ij=a_ij-a_i1·a^(l)_1j i = 2 , 3 , … , n

j = 1 , 2 , ... , n + 1

обеспечивает равенство нулю всех коэффициентов в 1-ом столбце матрицы А, за исключением а⁽¹⁾₁₁ ,который равен 1.

Фактически не нужно вычислять элемент, который становится равным нулю. Элементы теперь не занимают память ЭВМ и вычисления начинаются с j = 2.

В вычислительной технике принято оценивать эффективность алгоритмов числом операций, причем каждая операция представляет комбинацию умножения и вычитания. Можно показать, что исключение по Гауссу ~ n³/3, требует выполнения операций, где n - порядок матрицы, а обратная подстановка может быть выполнена n³/2 операций.

ПРИМЕР.

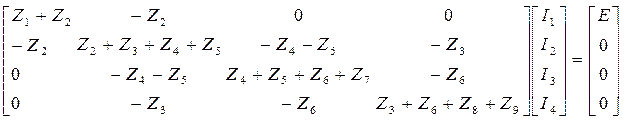
Z₁=1, Z₂=2, Z₃=1, Z₄=2, Z₅=1, Z₆=2, Z₇=1, Z₈=3, Z₉=2, E=2

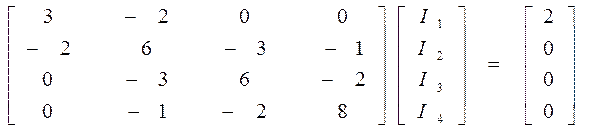
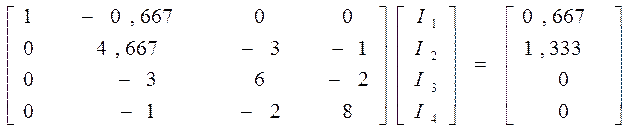
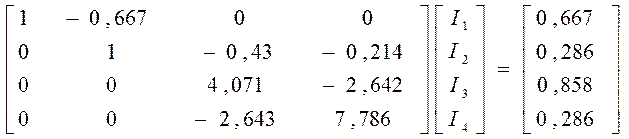
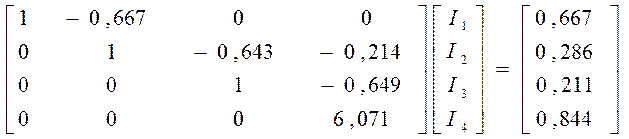
I₄=0,139, I₃=0,301, I₂=0,509, I₁=1,0065