Основной принцип получения теоретических распределённых моделей заключается в использовании фундаментальных физических законов.
К ним относятся законы сохранения массы, энергии, количества движения. Указанные законы в общем случае записываются в виде:
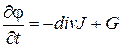, где
φ – некоторая фазовая переменная (плотность, энергия, импульс)
J = (Jx, Jy, Jz) – вектор потока фазовой переменной;
G – скорость генерации (массы, энергии, количества движения);
t – время.
divJ=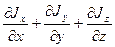 
- дивергенция вектора потока J (расхождение), которая характеризует сумму притока – стока через поверхность элементарного объёма.
В основе получения теоретических сосредоточенных моделей также лежат известные законы. Например, для моделирования механических поступательных систем используется основной закон динамики поступательного движения - производная по времени от количества движения системы относительно инерциальной системы отсчёта равна вектору всех внешних сил, приложенных к системе. В векторной форме закон имеет вид:
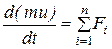, где
m – масса;
u – скорость.
Для электрических систем основными законами получения функциональных математических моделей являются:
Первый закон Кирхгофа: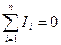 
Второй закон Кирхгофа: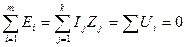 
Закон Ома: U=IR
