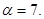Пример 2: Векторы  и
и  образуют угол j =
образуют угол j =  Найти длину вектора
Найти длину вектора  = 2
= 2  - 3
- 3  , если
, если  = 2,
= 2,  = 1.
= 1.
Решение. Согласно свойству скалярного проиведения, квадрат длины вектора  равен его скалярному квадрату. Найдем скалярный квадрат вектора
равен его скалярному квадрату. Найдем скалярный квадрат вектора  :
:
 = 4
= 4 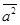 - 12
- 12 
 + 9
+ 9  = 4
= 4  - 12
- 12 
 cos j + 9
cos j + 9  = 4 * 2 2 – 12 * 2 * 1 cos (
= 4 * 2 2 – 12 * 2 * 1 cos (  ) + 9 * 12 = 16 –12+ + 9 = 13. Следовательно,
) + 9 * 12 = 16 –12+ + 9 = 13. Следовательно,  =
= 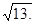
Пример 3:Найти угол ÐА в треугольнике с вершинами А (1; 2; - 1), В (5; 5; 11), С (13; 18; 20).
Решение. Искомый угол – это угол между векторами  =
= 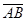 = {4;3;12} и
= {4;3;12} и  =
= 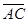 = {12;16;21}. По формуле (§3, следствие 2 ) имеем:
= {12;16;21}. По формуле (§3, следствие 2 ) имеем:
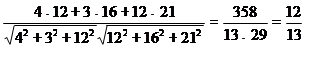
CosÐ А =
Таким образом, угол ÐА = arccos (  ) » 23 0 .
) » 23 0 .
Пример 4: Даны вершины треугольника: А(2;-1;3), В(1;1;1), С(0;0;5). Найдите длину стороны АВ и  .
.
Решение: Найдем координаты вектора, зная координаты его начала и конца:

 ,
,  .
.
 ,
,  ,
,
 ,
,  ,
, 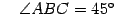 .
.
Ответ:  ,
, 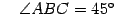 .
.
Пример 5:  Найти
Найти 
Решение. Воспользуемся формулой
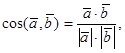
где  – скалярное произведение векторов
– скалярное произведение векторов 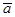 и
и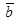 .
.
Вычислим  :
:
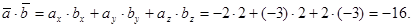
Найдем модули векторов
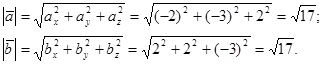
Тогда
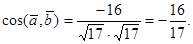
Пример 6.
Вектор ортогоналенвектору
ортогоналенвектору  Найти
Найти 
Решение.
Так как вектор 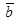 ортогонален вектору
ортогонален вектору  ,то
,то  , и, значит, скалярное произведение этих векторов тоже равно нулю:
, и, значит, скалярное произведение этих векторов тоже равно нулю:
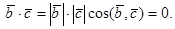
С другой стороны
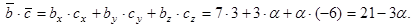
Итак,
 и
и