Пусть в пространстве задана прямоугольная система координат Охуz и произвольный вектор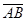 
. Пусть, далее, Х=ПРх 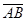, У=ПРу 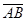, Z=ПРz 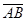(2). Проекции Х, У,Z вектора 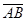на оси координат называют его координатами. При этом принята запись 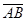= {C;U;Z}.
Теорема 2:Каковы бы ни были две точки А (х1; у1;z1) и В (х2; у2;z2), координаты вектора 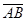определяются следующими формулами: Х=х2- х1 , У = у2 – у1, Z = z2 – z1. Другими словами, чтобы найти координаты вектора, если известны координаты начала вектора и его конца, надо из координат конца вектора вычесть соответствующие координаты начала вектора.
Доказательство: Поведем через точки А и В плоскости, перпендикулярные оси Ох, и обозначим точки пересечения с осью Ох соответственно через А/ и В/. Точки А/ и В/ на оси Ох имеют координаты х1 и х2
z
А В
х
у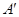 
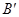
По определению, Х = ПРх 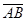= А/В/. Но А/В/ =х2 – х1. Поэтому Х=х 2– х. Аналогично устанавливаются и остальные формулы. g
Замечание: Если вектор 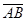выходит из начала координат, т. е. х1=у1=z1=0, и х2=х, у2=у, z2=z, то координаты Х, У,Z вектора 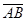равны координатам его конца: Х = х, У = у, Z =z.
