Каноническое уравнение имеет вид 
,
где 
и 
- это параметры параболоида, 
; 
,
Строим методом сечений.
1) Находим линию пересечения с плоскостью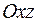 
.
Решаем систему уравнений
- это уравнение параболы, симметричной относительно оси 
.
2) Находим линию пересечения с плоскостью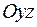 
.
Решаем систему уравнений
- это уравнение параболы,
симметричной относительно оси .
3) Находим линии пересечения с плоскостями, параллельными
плоскости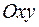 
.
а) Решаем систему уравнений
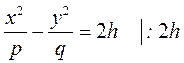
- это уравнение гиперболы, у которой
- действительная полуось, а 
- мнимая полуось.
б) Решаем систему уравнений
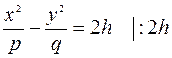
( знак левой части изменился, так как 
по условию)
- это уравнение гиперболы, у которой 
- действительная полуось, а 
- мнимая полуось.
4) Находим линию пересечения с плоскостью .
Решаем систему уравнений
- это уравнение двух прямых, проходящих через точку 
.
Гиперболический параболоид–это поверхность, имеющая вид седла.
