Рассмотрим частные случаи расположения плоскости  , определяемой общим уравнением:
, определяемой общим уравнением:  .
.
1. Если 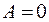 ,то
,то  .
.
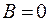 , то
, то  .
.
Если  , то
, то  .
.
Если  , то
, то  проходит через начало координат.
проходит через начало координат.
2. Если  , то
, то  .
.
Если  , то
, то  .
.
Если  , то
, то  .
.
3. Если 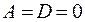 , то
, то  проходит через ось
проходит через ось 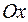 .
.
Если  , то
, то  проходит через ось
проходит через ось  .
.
Если  , то
, то  проходит через ось
проходит через ось  .
.
4. Если  - это уравнение плоскости
- это уравнение плоскости  .
.
Если  - это уравнение плоскости
- это уравнение плоскости  .
.
Если  - это уравнение плоскости
- это уравнение плоскости  .
.
5. Если  , то уравнение плоскости
, то уравнение плоскости  можно привести к виду :
можно привести к виду : 
 или
или  . Обозначив
. Обозначив  ,
,
получим  (3) – уравнение плоскости в отрезках на осях,
(3) – уравнение плоскости в отрезках на осях,
где 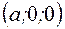 ,
,  ,
,  - точки пересечения с осями координат.
- точки пересечения с осями координат.
Примеры. Построить плоскости, заданные общими уравнениями:
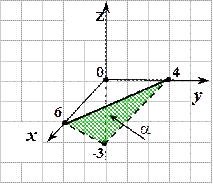
1. 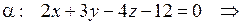
 .
.