Общее уравнение прямой на плоскости

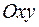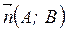Пусть в системе координат задана прямая , проходящая через точку , и задан вектор , перпендикулярный прямой .

Произвольная точка будет лежать на прямой 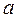, тогда и только тогда, когда , .

Из условия перпендикулярности векторов следует, что

(1) – уравнение прямой, проходящей через данную точку и перпендикулярной данному вектору.

Преобразуем уравнение (1):

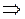
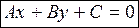
(2) – общее уравнение прямой.

Вектор называется нормальным вектором прямой .