Умножение матрицы 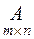 на матрицу
на матрицу  возможно, когда число столбцов первой матрицы (
возможно, когда число столбцов первой матрицы (  ) равно числу строк второй матрицы (
) равно числу строк второй матрицы ( 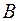 ).
).
 В результате получается матрица, число строк которой равно числу строк матрицы
В результате получается матрица, число строк которой равно числу строк матрицы  ; а число столбцов равно числу столбцов матрицы
; а число столбцов равно числу столбцов матрицы 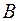 .
.
Схема: 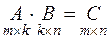
Определение. Произведением матриц  и
и  называется матрица
называется матрица  , каждый элемент которой
, каждый элемент которой  равен сумме произведений элементов
равен сумме произведений элементов  - й строки первой матрицы (
- й строки первой матрицы (  ) на соответствующие элементы
) на соответствующие элементы  - го столбца второй матрицы (
- го столбца второй матрицы ( 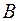 ).
).
Схема вычисления:









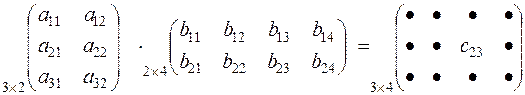
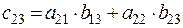
Например,  .
.
 .
.
В частном случае  .
.
Многие свойства операций над числами выполняются и для операций над матрицами:
1)  + + 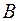 = = 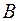 + + 
| 6) 
|
2)  +( +( 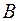 + +  )=( )=(  + + 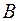 )+ )+ 
| 7) 
|
3) 
| 8) 
|
4) 
| 9) 
|
5) 
| |
Однако некоторые свойства произведения чисел не выполняются для произведения матриц:
- произведение  не всегда равно
не всегда равно  ;
;
(если  , то матрицы называются перестановочными).
, то матрицы называются перестановочными).
- произведение двух ненулевых матриц может равняться нулевой матрице: 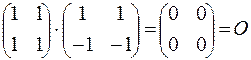 .
.