Пусть в линейном пространстве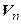 
по-прежнему заданы два базиса (3.46) и (3.47). Выберем в 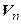произвольный вектор 
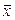. Его можно разложить как по одному базису, так и по другому: 
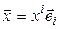и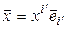 
. Тогда
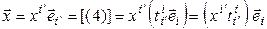. (3.49)
Равенство (3.49) – это разложение вектора 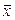по базису (3.46), и поэтому в силу единственности координат вектора в данном базисе получаем
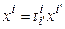. (3.50)
Обозначим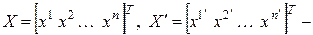 
координатные столбцы вектора 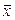в базисах (3.46) и (3.47) соответственно ( 
, 
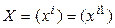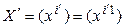). Тогда (3.50) равносильно равенству 
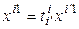, из которого вытекает, что
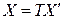. (3.51)
Формулы (3.50) и (3.51) показывают, как изменяются координаты вектора при изменении базиса. Равенство (3.51) можно доказать и так:
.
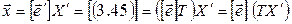Таким образом,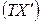 
– координатный столбец вектора 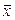в базисе (3.46), поэтому он совпадает с 
.
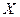