Пусть в линейном пространстве V задан некоторый базис, тогда каждый вектор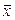 
можно разложить по этому базису.
Координатным столбцом вектора 
в заданном базисе будем называть столбец 
, составленный из координат вектора 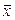в этом базисе.
Лемма 3.1.Для того чтобы векторы были линейно зависимыми, необходимо и достаточно, чтобы их координатные столбцы в некотором базисе были линейно зависимыми.
► Пусть заданы векторы
, (3.26)
– их координатные столбцы в некотором базисе. Одновременно проводим доказательство и необходимости, и достаточности. Согласно следствию из свойств координат векторов, координатный столбец линейной комбинации векторов равен такой же линейной комбинации координатных столбцов векторов-слагаемых. Имеем:
{(3.26) линейно зависима}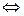 
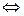
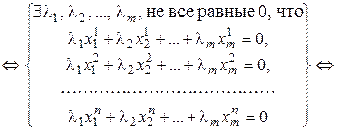
, не все равные нулю, что 
, не все равные нулю, что 
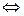{столбцы 
линейно зависимы}.◄
Теорема 3.1 (матричный критерий). Для того чтобы система векторов была линейно зависимой, необходимо и достаточно, чтобы ранг матрицы, составленной из координатных столбцов этих векторов в некотором базисе, был меньше количества векторов.
Для того чтобы система векторов была линейно независимой, необходимо и достаточно, чтобы ранг матрицы, составленной из координатных столбцов этих векторов, был равен их количеству.
Доказательство вытекает из леммы 3.1 и теоремы 2.4.
