Скалярное произведение векторов.

Скалярным произведениемвекторов а и b называется число, равное произведения длин этих векторов и косинуса угла между ними

а b = │а││b│cos (аb).

Скалярное произведение векторов обладает следующими свойствами: для любых векторов а,b, c и любого числа λ

1) а b = b a, 2) (a + b)c = a c + b c, 3) (λ a) b = a (λ b) = λ (a b).

Если известны координаты векторов а и b в ортонормированном базисе{i, j, k} а(а₁,а₂,а₃), b(b₁,b₂,b₃), то имеют место формулы

a b = а₁b₁ + а₂ b₂ + а₃b₃, │а│=

cos (а,b) =

1.33. АВСD – ромб с углом А равным 60° и стороной АВ равной 4. Найти скалярное произведение .

ОТВЕТ.. 8.

1.34. М – точка пересечения медиан равностороннего треугольника АВС со стороной равной 2. Найти скалярное произведение .

ОТВЕТ.. - .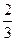

1.35. АВСD – квадрат стороной равной 5. Найти скалярное произведение .

ОТВЕТ. -25.