Скалярное произведение векторов

Скалярным произведением 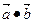двух векторов 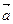и 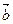называется число, равное произведению длин этих векторов на косинус угла между ними:

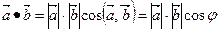(3.5).

Свойства скалярного произведения векторов:

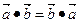
1.	4.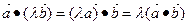
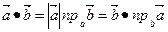
2.	5. 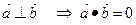Условие перпендикулярности векторов Векторы являются перпендикулярными тогда и только тогда, когда их скалярное произведение равно нулю.
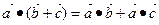
3.	6.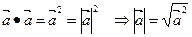

Проекцией вектора 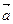на вектор 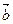называется число, равное

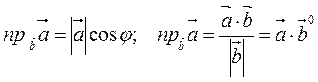(3.6).