Пусть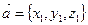 
и 
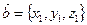
Тогда
1) 
;
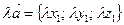2) 
;
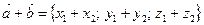3) 
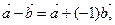т.е.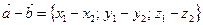 
.
Пример. 3.2.Найти координаты вектора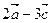 
, если 
.
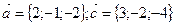Решение.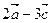 
.
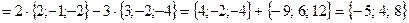Условие коллинеарности (параллельности)векторов
Для параллельности двух векторов необходимо и достаточно, чтобы координаты одного вектора были пропорциональны координатам другого
Векторы коллинеарны, если абсцисса первого вектора относится к абсциссе второго так же, как ордината первого — к ординате второго.
Формулы (1) и (2) кратко записывают в виде следующих пропорций:
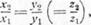соответственно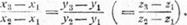 
Здесь один из знаменателей может оказаться равным нулю. Чтобы обойти эту трудность, договоримся всякую пропорцию понимать в смысле равенства ad = bс. Тогда обращение в нуль одного из знаменателей означает обращение в нуль и соответствующего числителя.
При этом обращение какого-нибудь из знаменателей в нуль означает, в соответствии с равенствами (1) или (2), что и числитель этой дроби равен нулю.
Понимать эти равенства надо с таким условием: если какой-то знаменатель равен нулю, то равен нулю и соответствующий числитель (про пропорциональность).
Из формулы вычеркиваются те из отношений, знаменатели которых равны нулю, а числители вычеркнутых отношений приравниваются нулю.
