Умножение вектора на число. Произведением вектора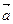 
на действительное число a называется вектор 
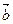такой, что 
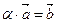. Вектор 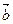удовлетворяет следующим условиям:
1) 
;
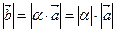2) направление вектора 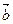совпадает с направлением вектора 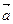, если 
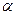положительное, и противоположно ему, если 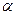отрицательное число;
3) 
.
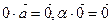Свойства:
· 
;
· 
;
· 
;
· 
.
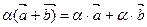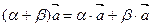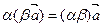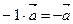• Обычно принято в записи произведения числа и вектора число записывать слева, но в принципе допустим и обратный порядок, хотя все же обычное соглашение состоит в том, чтобы его избегать, если нет прямой необходимости.
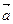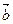Сложение векторов. Суммой векторов и называется вектор 
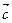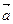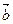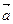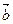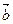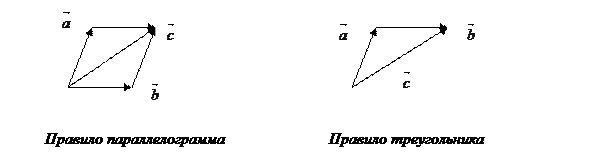
= + , начало которого совпадает с началом вектора , а конец – с концом вектора , при условии, что начало вектора совпадает с концом вектора 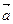(правило треугольников).
Очевидно, что вектор 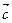в этом случае представляет диагональ параллелограмма, построенного на векторах 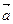и 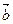(правило параллелограмма).
Свойства:
Вычитание векторов. Разностью двух векторов 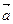и 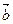называется = 
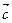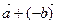, т.е.
.
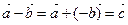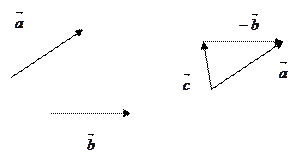
Таким образом, разностью векторов 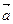и 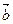называется вектор 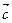, начало которого совпадает с началом вектора 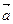, а конец – с концом вектора 
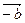, противоположного .
×
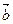