Кажуть, що точка М ділить відрізок [АВ] у відношенні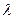 
,тобто 
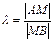, тому 
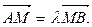Нехай А (х1,у1z1), В(х2,у2,z2). Тоді координати токи М (х; у; z) обчислюються за формулами
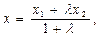
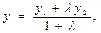
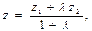(16)
Якщо точка М є серединою відрізка [АВ], тоб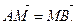то 
, то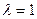 
і формула (16) набуває вигляду
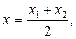
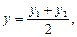
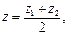(17)
Приклад 7. Відрізок з кінцями в точках А (3,-2)і В (6,4) розділено на три рівні частини. Знайти координати точок поділу.
Рис.6
Розв’язання:
Нехай С, D – точки поділу відрізка [АВ] на три рівні частини (малюнок дано). Зрозуміло, що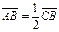 
. Тому точка С ділить відрізок [АВ] у відношенні 
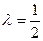. Використовуючи формули (16), знаходимо координати точки С:
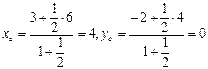, тобто С (4,0).
Із рівності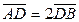 
випливає, що точка D ділить відрізок [АВ] у відношенні 
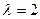. Тому координати точки D: 
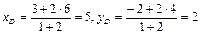D (5; 2).
Відповідь:Координати точки D (5;2), С (4,0).
Приклад 8. Знайти координати центра мас однорідної пластини, яка представлена у вигляді трикутника АВС, якщо А (5; 1; 13), В (11; 3; 8), С(2; 5; 0).
Розв’язання:
Центром мас трикутника є точка перетину медіан. Медіана – це відрізок прямої, який сполучає будь-яку вершину трикутника із серединою протилежної сторони.
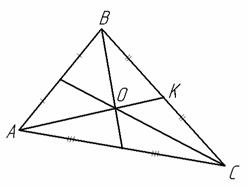
Рис.7
Тоді точка К є серединою відрізка ВС і її координати знаходимо за формулою (16):
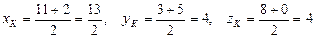
Медіани трикутника перетинаються в точці, яка ділить їх у відношенні 2:1, починаючи від його вершини. Якщо О – точка перетину медіан, то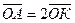 
, тобто λ=2 і за формулою (16) отримаємо:
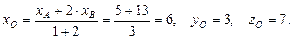
Отже, О(6; 3; 7).
Відповідь:Координати точки О(6; 3; 7).
