Розглянемо систему векторів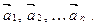 
Означення 4. Вектор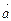 
називається лінійною комбінацієювекторів 
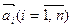, якщо існують такі числа 
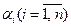, що
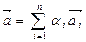(1)
Означення 5. Вектори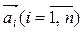 
називаються лінійно залежними, якщо існують такі числа 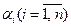, серед яких не всі дорівнюють нулю (тобто 
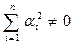), що справджується рівність
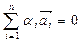(2)
Означення 6. Система векторів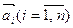 
називається лінійно незалежною, якщо рівність
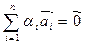(3)
можлива лише при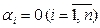 
.
Теорема 1. Для того, щоб система векторів була лінійно залежна необхідно і достатньо, щоб один з її векторів був лінійною комбінацією інших, тобто лінійно виражався через інші вектори системи.
Геометричний зміст лінійної залежності векторів в R3, що інтерпретуються як напрямлені відрізки, пояснюють слідуючи теореми.
