Критическое напряжение определяется по критической силе
δкр= Pкр/А=п^2*E*Imin\A(μl)^2
δпр=π^2*E*imin\μ*l^2
μ*l\imin=λ –гибкость стержня
δкр=π^2*E\λ^2
Гибкость стержня зависит от геометрических размеров и вида опор . Величина безразмерная. Критическое напряжение зависит от гибкости стержня и от упругих свойств материала. Критическое напряжение значительно меньше предела пропорциональности и предела текучести. Т.к потеря устойчивости может проходить при напряжениях значительно меньше чем при расчете на прочность.
Пределы применимости формулы Эйлера
Формула Эйлера применима при работе трения в упругой стадии, когда критическое напряжение меньше предела пропорциональности формула. Теперь можно получить предельную гибкость при которой и больше которой можно пользоваться ф-лой Эйлера.
δкр=π^2*E\λ^2
В дальнейшем стержни по гибкости будем разделять на 3 группы:
1.Стержень большой гибкости λ>λ0=100 δкр<δпр
Такие стержни рассчитываются на устойчивость по формуле Эйлера.
Fкр=π^2EImin\μl^2
2. Стержень средней гибкости. рассчитывается на прочность и устойчивость
λ=60:100
δр<δкр<δу
Для таких стержней применяется напряжение определяющееся по формуле Яшинского.
δпр=авλ
а и в постоянные для материала.
Для стали а=310МПА, в=1,41МПА
Fкр=δпр*А
3. Стержень малой гибкости Λ=0:60
Рассчитывается только на прочность δкр=δу
δ=F\A≤R
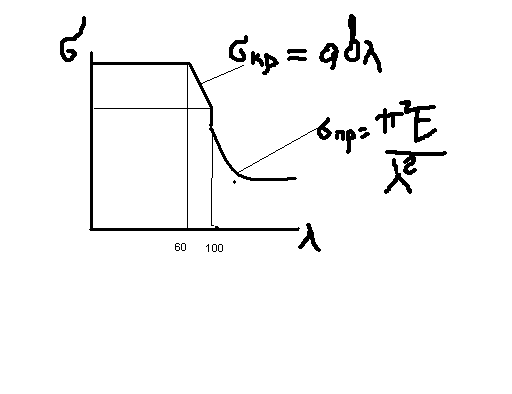
Можно построить график продольных напряжений для стали