Защемленная балка(рисунок)
,где х и у- главные ценр. оси поперечного сечения.
Раскладываем силу F на две составляющие Fx=F 
и Fy=F 
. Под действием Fy и Fx будут возникать два изгиб. момента, их эпюры (рисунок). Мх= Fy l ; Му= Fx l где z=l. Индекс у момента ставится вокруг какой оси поворачивается сечение т.о. косой изгиб можно рассматривать как сочетание двух плоских изгибов в главных плоскостях.
Нормальное напряжение в любой точке поперечн. сечения определяется формулой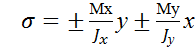 
, где х и у- координаты точки в главных центральных осях. Знак слагаемых устанавливается по характеру деформации, если точка испытывает растяжение от момента,то ставится знак +, если сжатие, то -. Для угловых точек 1,2,3,4 координаты принимают мах. Значение, поэтому формула для определения напряжений 
,где 
и
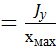. Наибольшее напряжение возникает в точках где суммируются напряжения одного знака.
