Как указывалось ранее, эти методы носят универсальный характер и используются в самых разных приложениях. Используется две основных идеи:
- одинаковые повторяющиеся данные можно заменить на короткую последовательность, состоящую из одного общего элемента и счетчика повторений;
- часто используемые значения кодируются короткими кодами, а редко используемые – более длинными кодами.
Первая идея довольно тривиальна, а вторая требует теоретического обоснования.
Точная связь между вероятностями и кодами установлена в теореме Шеннона [5]. Согласно этой теореме элемент 
, вероятность которого составляет 
, выгоднее всего представлять 
битами. Если при кодировании размер получаемых кодов всегда точно равен битам, то в этом случае длина закодированной последовательности будет минимально возможной. Если распределение вероятностей 
неизменно и вероятность появления элементов незовисимы, то можно найти среднюю длину кодов как среднее взвешенное
.
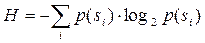Это значение также называется энтропией распределения вероятностей F или энтропией источника в заданный момент времени. Если известно распределение вероятностей элементов, генерируемых источником, то можно представить данные наиболее компактным образом, при этом средняя длина кодов может быть вычислена по формуле
,
где 
- вероятность того, что F примет k-е значение, т.е. 
, а энтропия примет значение 
.
