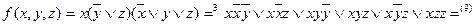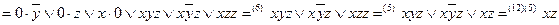Ассоциативность конъюнкции и дизъюнкции:
x1 · (x2 · x3) = (x1 · x2) x3 = x1 · x2 · x3
x1 v (x2 v x3) = (x1 v x2) v x3 = x1 v x2 v x3
Коммутативность конъюнкции и дизъюнкции:
x1 · x2 = x2 · x1 x1 v x2 = x2 v x1 (2)
Дистрибутивность дизъюнкции относительно конъюнкции:
x1 ( x2 v x3) = x1 · x2 v x1 · x3 (3)
Дистрибутивность дизъюнкции относительно конъюнкции:
x1 v (x2 · x3) = (x1 v x2) (x1 v x3) (4)
Идемпотентность:
x · x=x x v x=x (5)
Закон двойного отрицания:
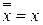(6)
Свойства констант 0 и 1:
x · 1 = x x v 1 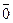= 1 
= 1
x · 0 = 0 x v 0 = x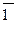 
= 0
Правила де Моргана:
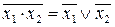
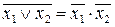(8)
Закон противоречия:
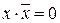(9)
Закон исключения третьего:
Основные эквивалентные соотношения (1 – 10) не выводимы друг из друга.
Наряду с ними для упрощения формул часто используются следующие эквивалентные соотношения, выводимые из основных эквивалентных преобразований:
- Поглощение:
x v x · y =x x(x v y) = x (11)
- Склеивание:
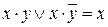(12)
- Обобщенное склеивание
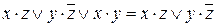(13)
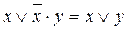(14)
Пример:
Упростить булевы формулы:
а)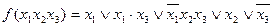 
Решение:
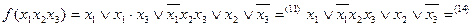
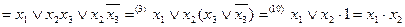
б) 
