Если в определителе второго порядка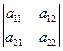 
его строки (столбцы) представить как
векторы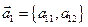 
, 
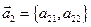, то модуль определителя равен площади параллелограмма, построенного на этих векторах. Доказательства вытекает из свойств векторного произведения двух векторов.
Если в определителе третьего порядка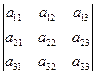 
его строки(столбцы) представить как векторы 
, 
, 
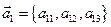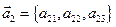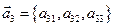, то модуль определителя равен объема параллелепипеда, построенного на этих векторах. Доказательства вытекает из свойств смешанного произведения трех векторов.
Литература
1. Общий курс высшей математики для экономистов: Учебник. /Под ред.В.И.Ермакова.-М.:ИНФРА-М,20001.-656с.
2. Головина Л.И. Линейная алгебра и некоторые ее приложения. - М.: Наука,1979.-392с.
3. Воеводин В.В., Кузнецов Ю. А. Матрицы и вычисления.- М.: Наука, 1984.-320с.
