Используются те же функции Maximize, Minimize, но они входят уже в блок решения Given и перед ними размещаются ограничения в виде равенств или неравенств, определяющие допустимую область значений параметров оптимизации.
В оптимизационных задачах с ограничениями решение целесообразно определять из необходимых условий экстремума. Эти условия порождают систему уравнений (чаще всего нелинейных), которые располагаются в блоке Given, вместе с ограничениями, определяющими допустимую область. Само решение ищется с помощью функций Find, Minerr.
Пример 5. Поиск точки минимума функционала Розенброка:
.
при ограничениях:
.
Документ MathCAD решения этой задачи показан на рис. 4.
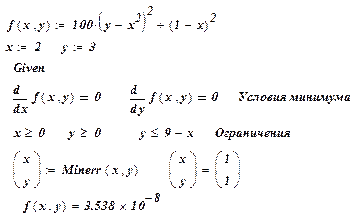
Рис. 4. Минимизация функции Розенброка при ограничениях
Пример 6. (задача линейного программирования). Цех малого предприятия должен изготовить 100 изделий трех типов 
и не менее 20 штук изделий каждого типа. На изделия уходит 4, 3.4 и 2 кг металла соответственно, при его общем запасе 340 кг, а также расходуются по 4.75, 11 и 2 кг пластмассы, при ее общем запасе 400 кг. Прибыль, полученная от каждого изделия равна 4, 3 и 2 р. Определить сколько изделий каждого типа необходимо выпустить для получения максимальной прибыли в рамках установленных запасов металла и пластмассы. Документ MathCad, решающий эту задачу приведен на рис.5.
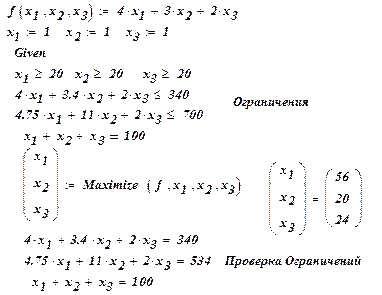
Рис. 5. Решение задачи с ограничениями
