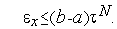Алгоритм золотого сечения.

Рассмотрим следующую задачу оптимизации: найти минимум одномерной унимодальной функции ( ), определенной в замкнутой области допустимых значений =[ , ],

( )= ( ).

Свойства золотого сечения.

Рассмотрим интервал [ , ]. Говорят, что точка c выполняет золотое сечение интервала [ , ], если

где = 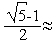0,618- решение квадратного уравнения

Алгоритм золотого сечения относится к классу последовательных методов поиска.

1. Выполняем присваивания , , , .
2. Вычисляем величины

Вычисляем значения функции ( ).

1. Если , то выполняем присваивания , , . Иначе - выполняем присваивания , ,
2. Если , то заканчиваем вычисления. Иначе - выполняем присваивание = +1 и переходим на п.2. Здесь – требуемая точность решения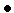

Рис. 3. К определению величин x₁^r, x₂^r.

В качестве приближенного значения точки минимума с равными основаниями может быть принята любая точка последнего текущего интервала неопределенности.

Количество итераций , необходимых для нахождения минимума функции с точностью , находится из условия