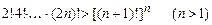1. Доказать формулу Sn = 12 + 22 + 32 + … + n2 =
= n(n +1)(2n +1) /6.
2. Обозначим Hn = 1 + 1/2 + 1/3 +…+ 1/n – гармонические числа. Доказать, что Нn неограниченно сверху, т.е. что Нn ® +¥ ( 
).
3. Доказать, что любую сумму денег более 7 копеек можно уплатить монетами достоинством 3 и 5 копеек.
4. Найти формулы для вычисления:
а)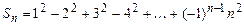 
б)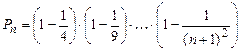 
Доказать формулы и утверждения (5 – 13).
5. 
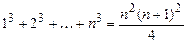
6. 
.
7. При любом х ¹ 1, 
.
8. Сумма кубов трех последовательных натуральных чисел n3 + (n + 1)3 + (n + 2)3 делится на 9.
9. Выражение 
делится без остатка на 9.
10. Число диагоналей выпуклого n-угольника k = n(n –2) /2.
11. Последовательность аn = 
(n корней) возрастает.
12. cos a×cos 2a×… ×cos 2na = 
.
13. 
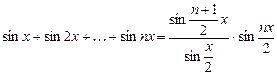
14. 
.
15. 
.
16. 
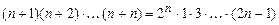
17. 
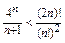
18. 
