Предположим, что имеется некоторое множество элементарных высказываний (типа 2 х 2 = 4). Будем обозначать их начальными буквами латинского алфавита. Введем в рассмотрение высказывательные переменные – символы, вместо которых можно подставлять высказывания. Их будем обозначать последними буквами латинского алфавита (x, y, z, ...).
Под формулами алгебры высказываний будем понимать осмысленные выражения, полученные из символов элементарных высказываний, символов высказывательных переменных, знаков операций и скобок.
П р и м е р ы .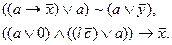 
Определение:
- Элементарные высказывания, символы логических переменных – формулы;
- Если F1 и F2 – формулы алгебры высказываний, то
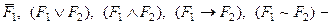формулы алгебры высказываний.
- Других формул алгебры высказываний нет.
Замечание: Для упрощения формул алгебры высказываний приняты следующие упрощения.
- Наружные скобки в записи формул можно опустить.
- Считается по определению, что конъюнкция «сильнее» дизъюнкции, а обе они «сильнее» → и ~. Поэтому часть скобок, определяющих порядок действий, можно опустить.
- Скобки, определяющие порядок действий в ассоциативном случае можно опустить.
- Конъюнкцию будем обозначать ∙или опускать.
Например, упрощенная запись формулы
.
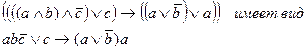П р и м е р 1 .С помощью равносильных преобразований доказать равенство: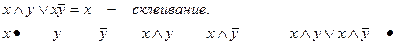 
0 0 1 0 0 0
0 1 0 0 0 0
1 0 1 0 1 1
1 1 0 1 0 1
П р и м е р 2.
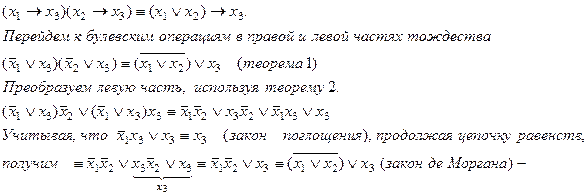
что и требовалось доказать.
