Множество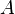 
является подмножеством множества 
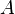, если любой элемент, принадлежащий , также принадлежит . Формальное определение:
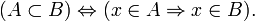
Множество называется надмно́жеством множества 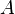, если 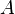— подмножество .
Пример множеств. Пустое и универсальное множества.
Термин "множество" употребляется как синоним понятий совокупность, собрание, коллекция некоторых элементов. Так, можно говорить о:
а) множестве пчёл в улье,
б) множестве точек отрезка,
в) множестве вершин квадрата или о множествах его сторон и диагоналей,
г) множестве студентов в аудитории и т.д.
В приведённых примерах в случаях а), в)-г) соответствующие множества состоят из определённого конечного числа предметов, такие множества называются конечными. Множество точек отрезка (пример б)) пересчитать невозможно, поэтому такие множества называются бесконечными. Множество, не содержащее ни одного элемента, называется пустым множеством.
Универса́льное мно́жество —множество, содержащее все мыслимые объекты. Универсальное множество единственно.
Универсальное множество обычно обозначается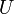 
, реже 
.
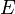