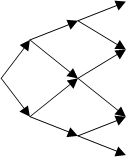
Предположим, что за каждый период времени, скажем час, стоимость некоторого актива S0 увеличивается или уменьшается. Пусть u > 1 – повышающий коэффициент, а d < 1 – понижающий, так что стоимость актива за единицу времени либо увеличивается и становится равной S0u, либо уменьшается и становится равной S0d. Если стоимость актива повышалась p раз и понижалась q раз, то его стоимость станет равной S0updq. При ud = 1 изменение стоимости актива может быть графически представлено так называемой биномиальной решеткой. На рис. 1 приведена трехпериодная биномиальная решетка.
S0u
S0u2
S0u3
S0u
 S0 S0
S0 S0
S0d
S0d
S0d2
S0d3
Рис. 1
Около каждого узла решетки указывается стоимость актива при соответствующем варианте развития событий. Максимальной стоимость актива окажется в том случае, когда в
каждом периоде его стоимость повышалась. Вообще, каждому варианту развития событий, при которых стоимость актива окажется равной S0updq, соответствует путь по стрелкам из
начального узла S0 в узел S0updq. Сопоставим каждому пути
последовательность букв d и u, в которой d соответствует понижению стоимости, а u – повышению. Число всевозможных путей из узла S0 в узел S0updq равно числу способов расставить p
букв u на p + q местах, т. е. числу сочетаний
C p q .