Алгоритм Прима

Отличается от алгоритма Краскала тем, что на каждом шаге строится не просто граф без циклов, но дерево.

1. Упорядочиваем ребра графа в порядке неубывания их весов.

2. Строим пустой граф 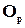, где - количество вершин исходного графа

3. На каждом шаге к текущему, уже сформированному графу, добавляем ребро исходного графа с минимальным весом. Ребро не должно образовывать цикл и нарушать связность. Для этого список ребер каждый раз просматривается, начиная с 1 ребра.

4. Алгоритм заканчивает работу, если количество ребер в формируемом графе станет равным .

Пример: алгоритм Прима

Список ребер

e₁=(1, 2), (4, 3) - 1

e₂=(1, 5) - 2

e₃=(4, 5) - 3

e₄=(1, 3), (2, 3) - 4

e₅=(2, 4) - 5

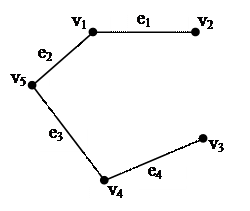
Остов кратчайших маршрутов: M=((1, 2), (1, 5),(5,4), (4,3))

Общий суммарный вес = 7.