1. Способ обхода в глубину
Поиск в глубину подразумевает просмотр ветвей дерева.
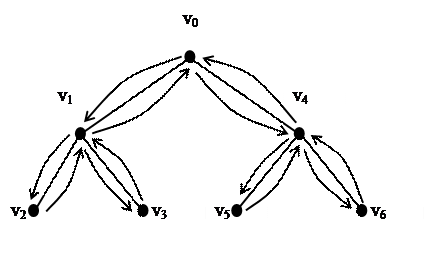
Начинаем поиск с некоторой фиксированной вершины 
.
Находим вершину 
смежную с и повторяем весь процесс, начиная с вершины :
- если существует не просмотренная вершина, смежная с вершиной , рассматриваем ее и, начиная с нее, выполняем поиск;
- если не существует ни одной новой вершины, смежной с , то говорят, что вершина использована, и делается возврат в вершину, из которой мы попали в вершину и продолжаем процесс;
- если на каком-то шаге 
, и нет ни одной использованной вершины, то алгоритм заканчивает работу.
2. Способ обхода в ширину
Подразумевает просмотр вершин по ярусам в иерархическом представлении. Здесь под использованием вершины подразумевается просмотр всех «соседей» данной вершины.
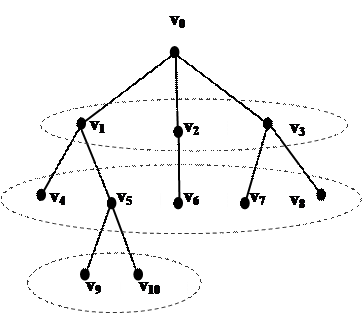
Остовы
(наличие деревьев в произвольном графе)
Остов (каркас, скелет) графа G– это остовный подграф графа G, задающий дерево на каждой компоненте связности графа G.
Для связного графа остов – это дерево, покрывающее все вершины исходного графа.
Пусть есть некоторый граф 
:
: остовы:
Ребра остова 
некоторого графа называются ветвями, а ребра графа , не вошедшие в ост, называются хордами.
