Дерево–связный граф, не содержащий циклов.
Лес (ациклический граф)– произвольный граф, не содержащий циклов. Компонентами леса являются деревья.
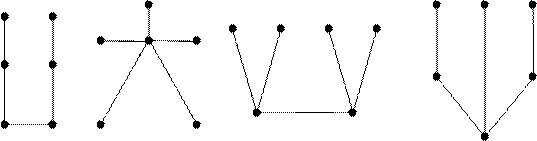
Теорема о дереве (5 различных определений дерева)
Для любого 
-графа 
следует, что утверждения (1-5) эквивалентны:
1. Граф – дерево, связный ацикличный граф.
2. Любые две несовпадающие вершины графа соединены единственной простой цепью.
3. Граф – связен, и количество ребер в нем на 1 меньше, чем количество вершин: 
.
4. Граф – ацикличен, и .
5. Граф – ацикличен, и если любую пару его несовпадающих несмежных вершин соединить ребром 
, то полученный граф 
будет содержать ровно один цикл.
