ФАЛ можно представить в виде n-мерного единичного куба: если наборам значений аргументов сопоставить точки n-мерного пространства, то множество 2n наборов определяет множество вершин n-мерного куба.
Одномерный куб (n = 1)
Функция принимает значения либо 0, либо 1.
F=0 – пустой кружёчек,
F=1 – закрашенный кружёчек.
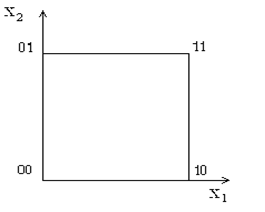
Двумерный куб (n = 2)
Трехмерный куб (n = 3)
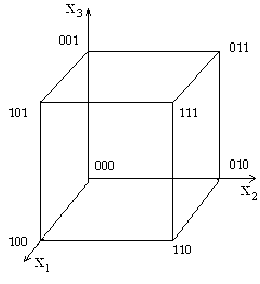
Таким же способом можно задать функцию от четырех переменных, в виде четырехмерного куба.
Четырехмерный куб (n = 4)
