Операции над частями графа

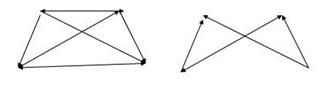
Граф Н называется частью графа G (H Ì G), если V(H) Ì V(G) и Е(Н) Ì Е(G).

Если V(H) = V(G), часть Н графа G называется суграфом. Суграф Н является покрывающим для н-графа G, если любая вершина графа G₁ инцидентна хотя бы одному ребру из Н.

Подграфом G(V¢) графа G(V) с множеством вершин V¢ Ì V называется часть, которой принадлежат все ребра с обоими концами из V¢.

Над частями графа G можно производить следующие операции:

- дополнение (определяется множеством ребер) Н: Е(Н)∩Е(Н) = Æ, Е(Н)UЕ(Н) = Е(G);

- сумма Н₁UН₂, Н₁ Ì G, Н₂ Ì G

V(Н₁UН₂) = V(Н₁)UV(Н₂) и Е(Н₁UН₂) = Е(Н₁)UЕ(Н₂)

- произведение Н₁∩Н₂:

V(Н₁∩Н₂) = V(Н₁)∩V(Н₂) и Е(Н₁∩Н₂) = Е(Н₁)UЕ(Н₂)

Если V(Н₁∩Н₂) =Æ Þ Е(Н₁∩Н₂) =Æ

Н₁ и Н₂ не пересекаются по ребрам, если Е(Н₁)UЕ(Н₂) =Æ, если V(Н₁)∩V(Н₂) =Æ, то сумма Н₁UН₂ называется прямой.