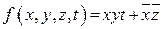Среди устройств дискретного действия встречаются схемы, закон функционирования которых определен не полностью. В таких схемах некоторые комбинации сигналов на входы никогда не подаются. Эти комбинации называются запрещенными.
Логическая функция называется неполностью определенной, если ее значения определены лишь на 
наборах аргументов.
На тех наборах, на которых функция не определена, ее можно доопределить произвольно таким образом, чтобы соответствующая функции схема была наиболее простой, то есть так, чтобы МДНФ доопределенной функции содержала наименьшее число букв.
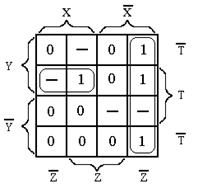
На карте Карно недоопределенное условие обозначается прочерком в соответствующей ячейке. Любую из таких ячеек можно включать как в группу единичных, так и в группу нулевых ячеек.
Пример. Функция 
задана таблицей
| x
| 0
| 0
| 0
| 0
| 0
| 0
| 0
| 0
| 1
| 1
| 1
| 1
| 1
| 1
| 1
| 1
|
| y
| 0
| 0
| 0
| 0
| 1
| 1
| 1
| 1
| 0
| 0
| 0
| 0
| 1
| 1
| 1
| 1
|
| z
| 0
| 0
| 1
| 1
| 0
| 0
| 1
| 1
| 0
| 0
| 1
| 1
| 0
| 0
| 1
| 1
|
| t
| 0
| 1
| 0
| 1
| 0
| 1
| 0
| 1
| 0
| 1
| 0
| 1
| 0
| 1
| 0
| 1
|
| f
| 1
| –
| 0
| –
| 1
| 1
| 0
| 0
| 0
| 0
| 0
| 0
| 0
| –
| –
| 1
|
